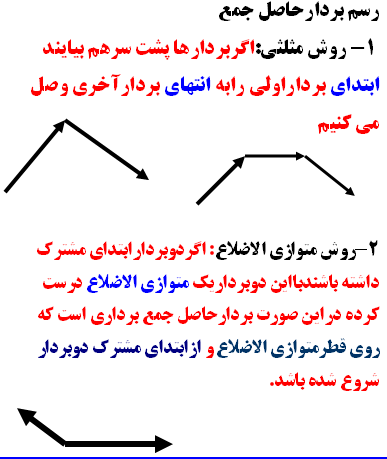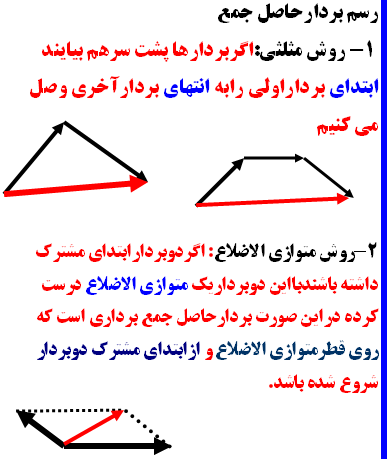
رسم بردارحاصل جمع ویژه دانش آموزان سال سوم راهنمایی

اشکال جدید هندسی ( همراه انیمیشن)

الف) دلگون(Cardioid) :اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع 1 واحد، حول آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را دلگون گويند . 

نفروئيد(Nephroid):  اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع2 واحد، حول آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را نفروئيد گويند

 ج)دلتاگون(Deltoid):  اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع3 واحد، درون آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را دلتاگون گويند

 

د)ستاره گون(Astroid):  اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع4 واحد، درون آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را ستاره گون گويند .

 

 

 در ادامه مي توانيد روش هاي ديگر رهيافت به اشكال فوق را ملاحظه نماييد :

 

 

 

 

 

خطای دید

ادامه نوشته

الگوريتم غربال اراتستن براي تعيين اعداد اول

الگوريتم غربال اراتستن براي تعيين اعداد اول سال سوم راهنمایی

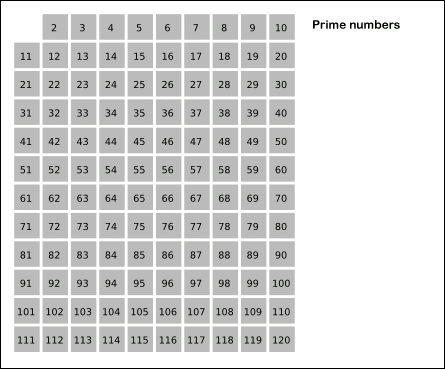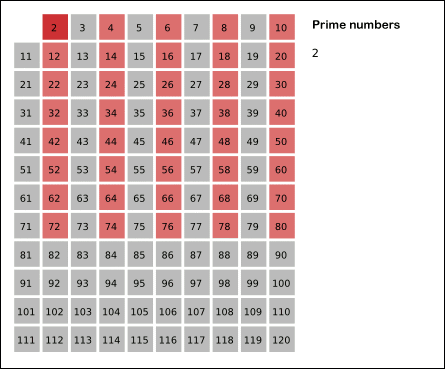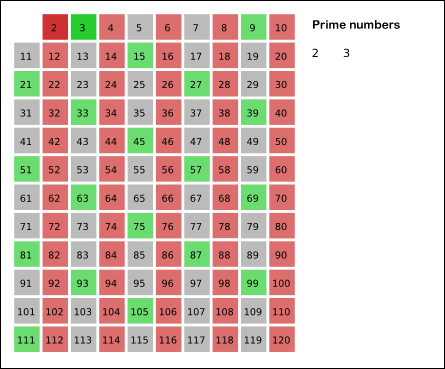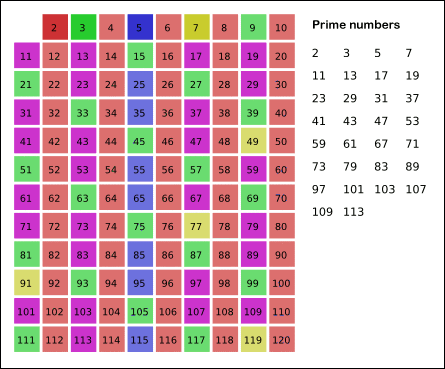
توضیح:

۱) رنگ قرمز مضرب های مرکب ۲ را نشان می دهد.

۲) رنگ سبز مضربهای مرکب عدد۳ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)

۳) رنگ آبی مضربهای مرکب عدد۵ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)

۴) رنگ زرد مضربهای مرکب عدد۷ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)

۵) رنگ بنفش اعداد اول را نشان می دهد.

 

 

انیمیشن قضیه ی تالس

قضیه ی تالس

تقريب هندسي پي

 

تقريب هندسي عدد پي

 

 

انيميشني كه روشي براي تقريب عدد پي ، ارائه مي كند ...

دايره اي به شعاع 1 واحد در نظر بگيريد . همان طور كه در شكل زير مي بينيم مساحت چند ضلعي هاي منتظم محاط در اين دايره با افزايش تعداد ضلع ها به سمت مساحت دايره كه همانا عدد پي مي باشد ، نزديك و نزديك تر مي شوند .

 

 

یک انیمیشن بسیار جالب دیگر برای بدست آوردن مقدار تقریبی عدد پی:

 

 

 

خطای دید!

زنگ تفریح:

به تصویر زیر با دقت نگاه کنید و بگوئید چند چهره در این تصویر مشاهده می کنید؟ لطفا خوب دقت کنید!

تست هوش تصویری(درخت)

اگر بین ۰ تا ۵ تصویر صورت پیدا کردید – سبک مغز

اگر ۶ یا ۷ تصویر صورت پیدا کردید – کند ذهن

اگر ۸ یا ۹ تصویر صورت پیدا کردید – معمولی

اگر ۱۰ یا ۱۱ تصویر صورت پیدا کردید – خیلی خوب

اگر ۱۲ یا ۱۳ تصویر صورت پیدا کردید – نابغه

 

فالی به زبان ریاضی

                                          

فالی به زبان ریاضی:

ازگزینه های زیر یکی را انتخاب بکنید وبه ادامه مطلب بروید:

مربع       مستطیل      مثلث   دایره      منحنی

 

ادامه نوشته

1=2؟!........

مسلما ۱ مساوی با ۱ است اما عکس زیر کاملا منطقی نشان دهنده آن است که یک مساوی با ۲ است. آیا کسی میتواند بگوید که چه ترفندی در اینجا به کار رفته و یا شاید هم ترفندی در کار نبوده و ۱ مساوی با ۲ است!!!

جالب بود!!! مگه نه؟

چطور ممکنه 64=65 باشه؟!

بدست آوردن سن،روز و ماه تولد شما

                  

بدست آوردن سن،روز و ماه تولد شما

عدد ماه تولد خود را انتخاب کنید.ضرب در ۱۰۰ کنید.

به اضاقه ی روز تولد کنید.

ضرب در ۲ کنید.

به اضافه ی ۶ کنید.

ضرب در ۵ کنید.

به اضافه ی ۴ کنید.

ضرب در ۱۰ کنید.

منهای ۳۴۰ کنید.

به اضافه ی سن خود کنید.

دو رقم اول از سمت راست سن/دو رقم دوم روز تولد/یک یا دو رقم باقیمانده سوم ماه تولد شما می باشد.

ترفندهای ضرب و تقسیم ریاضی (اعداد چند رقمی)

ترفندهای ضرب و تقسیم ریاضی (اعداد چند رقمی)

---

1 – عددهایی که به 5 ختم میشوند وضرب در مجذورشان می شوند؛ مثال:  ؟ = 85×85

قدم اول: قسمت اول عدد را در بعلاوه یک همان عدد ضرب کنید ؛   72 = (1+8)×8

قدم دوم: عدد 25 را جلو عدد بدست آمده تان بنویسید؛  7225

تمرین: ؟ = 15×15     ----      ؟ = 65×65

 

1 - Square numbers ending in 5

85 x 85 = 7225

Step 1 - Multiply the first digit by the first digit plus one: 8 x (8 + 1) = 72

Step 2 - Write the number 25 next to the number from the first step: 7225

45 x 45 = 2025

Step 1 - 4 x (4 + 1) = 20

Step 2 – 2025

---

 

2 _ ضرب عددهای دورقمی در 11 ؛ مثال: ؟ = 11×53

قدم اول: دو رقم یکان و دهگان عددی که قرار است ضرب در 11 شود را با هم جمع کنید؛ 8 = 3+5

قدم دوم: عدد بدست آمده را بین دو رقمی که با هم جمع زدید قرار دهید؛ 583

تمرین:   ؟= 11×78     ----     ؟= 39×11

2 - Multiply two digit number by 11

53 X 11 = 583

Step 1 - Add both digits of the two digit number: 5 + 3 = 8

Step 2 - Place the result in between both digits: 583

59 X 11 = 649

Step 1 - 5 + 9 = 14

Step 2 - Carry the 1 when the result is greater than 9: 5 + 1 = 6

Step 2 – 649

---

 

 

3 _ ضرب عددهای زوج در پنج؛ مثال:  ؟ = 5×242

قدم اول: عدد ضرب شده در 5 را تقسیم بر 2نمایید؛  121 =2÷242

قدم دوم: یک صفر آخر عدد بدست آمده در گام قبل قرار دهید؛  1210

تمرین:   ؟= 748×5    ----    ؟= 5×452

3 - Multiply even number by 5

242 x 5 = 1210

Step 1 - Divide the even number by two: 242 / 2 = 121

Step 2 - Put a 0 at the end of the result: 1210

---

 

4 _ ضرب اعداد  بین 10 تا 19؛ مثال:   ؟= 18×17

قدم اول: عدد بزرگتر را با یکان عدد کوچکترجمع کنید؛ 25 = 7+18

قدم دوم: یک صفر جلو نتیجه بدست آمده در مرحله قبل قرار دهید؛  250

قدم سوم: یکان دو عددی که در هم ضرب شده اند را در هم ضرب نمایید؛ 56 = 8×7

قدم چهارم: جواب بدست آمده از مرحله دوم و سوم را با هم جمع نمایید؛ 306 = 250+56

تمرین:   ؟ = 12×15     ----       ؟ = 19×16

4 - Multiply between 10 and 19

18 x 17 = 306

Step 1 - Add the larger number to the rightmost digit of the other number: 18+ 7 = 25

Step 2 - Put a 0 at the end of the result from step 1: 250

Step 3 - Multiply the rightmost digits of both original numbers: 8 x 7 = 56

Step 4 - Add steps 2 and 3: 250 + 56 = 306

 

---

5 _ تقسیم اعداد چند رقمی بر 5 ، 50 ، 500 و ... ؛مثال:  ؟=5÷52

قدم اول: عددهایی را که تقسیم بر 5 ، 50 یا ...  می شوند را ضرب در 2 کنید؛   104 = 2×52

قدم دوم : جدا کنید عدد مرحله اول را با یک ممیز و به ازای هر صفر جلو 5 یک ممیز به عقب بروید؛ 10.4

تمرین:     ؟=50÷482    ----     ؟= 5 ÷1150

 

 5 - Divide by 5, 50, 500, etc..

52 / 5 = 10.4

Step 1 - Multiply the number being divided by two: 52 x 2 = 104

Step 2 - Shift the number from step 1 by one decimal point: 10.4

482 / 50 = 9.64

Step 1 - 482 x 2 = 964

Step 2 - Shift the number from step 1 by two decimal points (for dividing by 500 shift by three decimal points): 9.64

 

---

6 _ مجذور اعداد از ریشه 50؛مثال:  ؟= 58×58

قدم اول:عدد یکان ضرب را با 25 جمع کنید؛   33= 8+25

قدم دوم: عدد یکان را به توان 2 برسانید؛   64= 8 ×8

قدم سوم: عدد بدست آمده در قدم دوم را جلو گام اول قرار دهید؛  3364

تمرین:    ؟= 51 ×51     ----      ؟= 59 ×59

6 - Square numbers in the 50's

58 x 58 = 3364

Step 1 - Add 25 to the ones digit: 25 + 8 = 33

Step 2 - Square the ones digit number: 8 x 8 = 64

Step 3 - Place the result from step 2 next to the result from step 1: 3364

 

---

7 _ ضرب اعداد دو رقمی که رقم دهگان شان شبیه به هم و عدد یکانشان بین 1 تا 9 متفاوت است؛مثال:   ؟=38 ×32

قدم اول:عدد دهگان را ضرب در 1+ همان عدد نمایید؛   12=(1+3)× 3

قدم دوم:یکان دو عدد را ضرب در هم نمایید؛  16= 2 × 8

قدم سوم: نتیجه مرحله 2 را جلو مرحله یک قرار دهید؛    1216

تمرین:     ؟=75 ×79    ----     ؟= 43 ×44

7 - Multiply two digit numbers having same tens digit and ones digits add up to 10

38 x 32 = 1216

Step 1 - Multiply the first digit by the first digit plus one: 3 x (3 + 1) = 12

Step 2 - Multiply the rightmost digits (if the result is a single digit put a 0 in front of it): 8 x 2 = 16

Step 3 - Put the result from step 2 next to the result from step 1: 1216

 

---

8 _ ضرب در اعداد 9 ، 99 ، 999 و . . .؛ مثال:    ؟=56 ×99

قدم اول: به ازای هر 9 انتهای عدد ضرب شده در 9 صفر قرار دهید؛   5600

قدم دوم: عدد اولیه ی ضرب شده در 9 را ازعدد مرحله اول کم کنید؛     5544=56-5600

تمرین:    ؟= 48 ×99    ----     ؟=7 ×999

8 - Multiply by 9, 99, 999, etc..

56 x 99 = 5544

Step 1 - Place a zero at the end for each 9: 5600

Step 2 - Subtract the original number from step 1: 5600 - 56 = 5544

 

---

9 _ ضرب اعداد در 125 ؛ مثال:   ؟=125 × 68

قدم اول: سه صفر آخر عدد ضرب شده در 125 قرار دهید؛  68000

قدم دوم: عدد مرحله اول را تقسیم بر 2 نمایید؛   3400= 2 ÷ 6800

قدم سوم:عدد مرحله دوم را تقسیم بر 2 نمایید؛   1700= 2÷ 3400

قدم چهارم: عدد مرحله سوم را بر 2 تقسیم نمایید؛   8500=2÷ 1700

یا داریم: (خلاصه مراحل) 

قدم اول: سه صفر جلو عدد تک رقمی قرار داده؛

قدم دوم: عدد بدست آمده مرحله اول را تقسیم بر 8 نمایید؛

9 - Multiply by 125

68 x 125 = 8500

Step 1 - Place three zeros at the end of the number: 68000

Step 2 - Divide the number from step 1 by two: 68000 / 2 = 34000

Step 3 - Divide the number from step 2 by two: 34000 / 2 = 17000

Step 4 - Divide the number from step 3 by two: 17000 / 2 = 8500

 

 

---

10 _ مجذور اعداد در صورت دانستن مجذور عدد قبلی؛ مثال:   ؟= 61 ×61

قدم اول: پیدا کنید مجذور عدد قبلی را ؛  3600=60 ×60

قدم دوم: ضرب کنید عدد اولیه را در 2 سپس یک واحد از جواب بدست آمده کم نمایید؛   121=1 - (61 ×2)

قدم سوم: مرحله 2 را با مرحله 1 جمع نمایید؛    3721=3600+121

تمرین:    ؟= 51 ×51      ----       ؟= 91 ×91

 10 - Square numbers if you know the square of the previous number

61 x 61 = 3721

Step 1 - Find the square of the previous number: 60 x 60 = 3600

Step 2 - Multiply the number being squared by two and subtract one: (61 x 2) - 1 = 121

Step 3 - Add step 2 to step 1:    3600+ 121 = 3721

---

این مطلب ترجمه ای میباشد از نرم افزار شگفت انگیز Math Tricks Lite و شامل 10 ترفند اولیه این نرم افزار به همراه ترجمه میباشد ؛ تقدیم به تمام علم دوستان و دانشجویان و دانش آموزان؛

---

" پيروزی آن نيست که هرگز زمين نخوری، آنست که بعد از هر زمين خوردنی برخيزی"
 ((مهاتما گاندی))

---

ثابتی که گاهی اوقات زیر آبی می رود!

 

ثابتی که گاهی اوقات زیر آبی می رود! 

 در سال ۱۹۴۹ یک ریاضی‌دان  هندی به نام «کاپرکار» ویژگی جالبی را در اعداد کشف و در مقاله‌­­ای در همان سال منتشر کرد . او کشف خود را این طور توضیح داده‌بود : یک عدد چند رقمی انتخاب کنید (مثلا ۸۹۵۲) ، ارقام آن را یک بار به صورت نزولی مرتب کنید (۹۸۵۲) و  یک بار هم به صورت صعودی (۲۵۸۹) ، تا «بزرگترین» و «کوچکترین» عدد ، با همان ارقام حاصل آید.

ادامه نوشته

واژه ریاضیات و بهترین واژه جایگزین آن

                          

واژه ریاضیات و بهترین واژه جایگزین آن

واژه ریاضیات ، به جای واژه یونانی (( ماته ماتیکه )) Mathematike گذاشته شده است که خود از (( ماته ما )) Mathema به معنای (( دانش )) و (( دانایی )) آمده است.اغلب ، واژه (( ریاضیات )) را ، برگرفته از واژه (( ریاضت )) دانسته اند ؛ چرا که (( ریاضت )) تنها به معنای (( پرهیزکاری بدنی )) نیست و (( در خود فرو رفتن ))  و (( فهمیدن )) و (( رسیدن  به رازها )) را هم می رساند. 

ادامه نوشته

سخنان جالب از بزرگان ریاضی

ریاضیات حاکم علوم است ونظریه اعداد ملکه ریاضیات (گاوس)

چهل درصد ریاضیات تخیل است چهل درصد آن اثبات و چهل درصد ان خلاقیت!!!

بدون ریاضیات شاید هنر و ادبیات داشته باشیم ولی تکنولوژی و صنعت هرگز

چیزی در جهان وجود ندارد که با عدد قابل بیان نباشد (فیثاغورس)

به کمک اعداد می توان زندگی وپیشامد های ان را پیش بینی کرد (فیثاغورس)ژاكوبی)
با وجود اهمیتی كه كاربرد ریاضیات دارد اما این كار نباید ملاك ارزش گذاری آن باشد.
(هیلبرت)
به نظر میرسد معمار بزرگ جهان ریاضیدان است.
(جینز)
زندگانی به این درد می خورد كه انسان به دو كار مشغول گردد :
اول : ریاضی بخواند.
دوم : ریاضی درس بدهد.
(پواسون)
در هر چیز از جمله یك نظریه ریاضی زیبایی را میتوان درك كرد اما نمی توان توضیح داد.
(كیلی)

چنین به نظر می رسد كه ریاضیات حس جدیدی غیر از احساسات عادی به ریاضیدان می بخشد.

فلیکس کلاین
افلاطون گفت : خدا هندسه دان است ، ژاکوبی این جمله را چنین تغییر داد : خدا حساب دان است ، سپس کرونکر آمد و این سخن به یاد ماندنی را باب کرد : خدا عدد های طبیعی را آفرید ، ما بقی کار انسان است

خیام
ریاضیات، به پیشگامی سزاوارتر است

جان لاک

اثبات ریاضی مانند الماس قاطع و شفاف است، و با چیزی جز استدلال دقیق نمی توان به آن رسید.

هفت های مهم

*رنگین کمان 7 رنگ دارد .

*عجایب جهان 7 تا هستند .

* سوره حمد که اولین سوره قرآن است 7 آیه دارد .

* آسمان 7 طبقه دارد .

*موسیقی ایران و یونان 7 دستگاه دارد .

* 7 نوع ساز بادی وجود دارد .

* 7 نت موسیقی وجود دارد .

* ایرانیان برای اهورامزدا 7 صفت نیک بر می شمردند .

* سفره سال نو 7 س دارد .

* عرفای بزرگ برای عشق و وصال 7 مرحله طی می کنند .

* طواف نیز 7 بار است .

هفت سین ریاضی

شگفتیها وزیبایهای ریاضی:توان

ه تساوی زیر نگاه کنید :

 

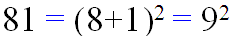
بله 81 برابر است با توان دوم ِ مجموع ارقامش.

آیا اعداد دیگری با این ویژگی وجود دارند؟

به عدد زیر نیز توجه کنید :

 

حتما ً شگفت زده شده اید !

در این قسمت می خواهیم اعدادی را معرفی کنیم که این اعداد با توانی از مجموع ِ ارقامشان برابرند. البته در این میان، اعداد یک رقمی با مجموع ارقامشان به توان ۱ برابند و از آن ها چشم پوشی می کنیم. یافتن اعداد کوچک با این ویژگی کار ساده ای است اما یافتن اعداد بزرگتر بسیار مشکل و زمان بر خواهد بود. در جدول زیر تعدادی از این اعداد را به نمایش در آورده ایم . ببینید و لذت ببرید :

اعجاز و شگفتیهای ریاضی در قران

شگفتیهای ریاضی قرآن

كتاب عبدالرزاق نوفل اعجاز عددى در قرآن‏كریم نام دارد و به قلم قرآن‏پژوه و قرآن‏شناس دانشور معاصر، آقاى مصطفى حسینى طباطبائى به فارسى ترجمه شده است.

 ذیلاً تعدادى از آمار و ارقام شگفت‏آور عبدالرزاق نوفل نقل مى‏شود:

- واژه دنیا در قرآن كریم 115 بار به‏كار رفته است، و واژه آخرت هم همین تعداد.

- شیاطین 68 مرتبه، ملائكه هم همین تعداد.

- حیات 71 بار، موت هم همین تعداد.

- علم و معرفت ومشتقات آنها 811 بار، ایمان و مشتقات آن‏هم همین تعداد.

- ابلیس یازده بار، و استعاذه از او هم به‏همین تعداد.

- كلمه یوم به‏معناى روز(به‏صورت مفرد) 365بار به‏تعداد روزهاى‏سال (شمسى) در قرآن به‏كار رفته است. و به‏صورت تثنیه و جمع سى بار، به‏تعداد روزهاى ماه.

- كلمه شهر به‏معناى ماه، 12 مرتبه در قرآن دیده مى‏شود به‏تعداد ماه‏هاى سال.

اما كتاب دكتر ابوزهراء النجدى قرآن‏پژوه شیعه من الاعجاز البلاغى و العددى للقرآن الكریم نام دارد و چنان‏كه از نامش برمى‏آید به‏عربى است و هنوز به‏فارسى ترجمه نشده است و از نظر شگفتى‏هاى ریاضى به‏پاى كار رشاد خلیفه و عبدالرزاق نوفل نمى‏رسد.

ذیلاً چند تناسب و ظرافت عددى قرآنى را كه او پیدا كرده و در كتاب پیش گفته آورده است، نقل مى‏كنیم:

- ساعت/ الساعة در قرآن كریم 24 بار به‏كار رفته است به تعداد ساعات شبانه‏روز.

- سماوات السبع یا سبع سماوات، هفت بار به‏كار رفته است.

- «سجد» و مشتقات آن 34مرتبه به‏كار رفته است كه برابر مجموع سجده‏هاى هفده ركعت نماز شبانه‏روزى است، از قرار هر ركعتى دو سجده، جمعاً 34 سجده.

- لفظ صلاة و قیام و اقیموا و مشتقات آن 51 بار به‏كار رفته است كه برابر با هفده‏ركعت نماز واجب و 34 ركعت نماز مستحب شبانه‏روزى است.

- مشتقات وصى/ توصیه به‏تعداد اوصیاى الهى دوازده بار به‏كار رفته است.

- لفظ شیعه و مشتقاتش دوازده بار در قرآن به‏كار رفته است.

- مشتقات فرقه، 72 بار به‏كار رفته است و این به‏تعداد 72 فرقه اسلامى است.

در پایان این نكته گفته شود كه این‏گونه پژوهش‏ها جنبه تفننى دارد، و ارزش طراز اول علمى ندارد.

ساعت ریاضی

 

 

ساعت ریاضی:

 

                                                             

 

زیبایی و ریاضیات

زیبایــی و ریاضیــات :)

                     

گیاه آلوئه پلی فیلا - Aloe Polyphylla - یکی از گیاهان سبزی است که به صورت مارپیچ رشد می‌کند و در حد نهایت رشد خود، تقارن زیبایی را پدید می‌آورد .

عجایب عدد هفت

                                        

عدد هفت عددی است که شاید مثل همه ی عدد های دیگر در نظر ما عادی جلوه کند اما نگرش ما وقتی متبلور می شود که خواص عدد هفت را بدانیم و ببینیم چه «هفت» هایی در زندگی ما وجود دارند و ما در گیر و دار زندگی ماشینی و با بی تفاوتی از کنار آن ها رد می شویم مثلا شاید جالب باشد که بدانیم، رنگین کمان دارای هفت رنگ است .
عجایب جهان، هفت تا هستند.(که به عجایب هفت گانه معروفند ) یا در یونان باستان، اسطوره ای با نام هفت خدای، در ذهن مردم نقش بسته است، ویا شهر عشق، که دراشعار عطار آمده است، هفت شهر می باشد، سوره ی مبارکه حمد، که اوّلین سوره ی قرآن کریم است، هفت آیه دارد. آسمان دارای هفت طبقه است. بهشت وجهنم هر کدام دارای هفت طبقه و درجه هستند و طواف خانه خدا هفت دور است، موسیقی ایران و یونان هفت دستگاه داد، هفت نوع ساز بادی وجود دارد و علاوه بر این هفت نت موسیقی وجود دارد(دو، ر، می، فا، سل، لا، سی) و…

تاریخچه:
در سال ۱۸۸۹ میلادی کتابی ار یک جهان گرد منتشر شد که، از جمله روش شمردن را در میان قبیله ای از تورس شرح داده است. اینها برای شمردن تنها از دو واژه استفاده می کردند: یک و دو. برای عدد سه می گفتند «دو و یک » برای چهار «دو و دو»، برای پنج «دو و دو یک » و برای شش «دو و دو و دو» ولی برای عددهای بزرگ تر از ۶، هر قدر بود، می گفتند «خیلی ». گرچه این آگاهی مربوط به پایان سده ی نوزدهم است ولی می تواند گواهی بر شیوه ی شمردن در آغاز شکل گیری مفهوم عدد در میان انسان های نخستین باشد.
بعد ها که برای عددهای بزرگتر هم نامی در نظر گرفتند به احتمالی برای عدد «هفت» از همان واژه ی قبلی «خیلی» یا «بسیار» استفاده کردند. عدد هفت که سده های متوالی برای آنها نا شناخته بود، اندک اندک به صورت عددی مقدس در آمد. وقتی که مصری ها، بابلی ها و دیگر امت ها توانستند پنج سیاره ی نزدیک تر به خورشید را بشناسند، با اضافه کردن ماه و خورشید، به عدد هفت رسیدند و این بر تقدس عدد ۷ افزود وقتی در قصه های کهن تر، که تا زمان ما هم ادامه پیدا کرده است، صحبت از شهری می شود که هفت برج و هفت بارو داشت، به معنای آن است که این شهر برج و باروهای بسیار داشت. هفت آسمان و هفت دریا و هفت کشور، به معنای آسمان ها و کشور ها و دریاهای بزرگ است نه هفت آسمان و هفت دریا (نه کم و نه زیاد ).
هنوز در زبان فارسی اندرز می دهند « هفت بار گز کن یک بار پارچه کن ». این جمله به معنای آن نیست که برای دقت کار و کم کردن اشتباه در اندازه گیری یا هر کار دیگری باید درست ۷ بار آزمایش کرد، نه شش یا هشت بار. در اینجا هم هفت به معنی «بسیار» است. عدد۱۳ هم چنین سرنوشتی دارد…

تعدادی از مشهورترین 7 های جهان عبارتند از:
هفت طبقه بهشت:
بر اساس آیات قرآن و مفسران احادیث، بالاترین درجه سعادت معنوی، ورود به طبقه هفتم بهشت است. مسلمانان به وجود هفت طبقه یا مرحله آمرزش و بهشتی شدن اعتقاد دارند. این طبقات هفتگانه همانهایی هستند که طی شده است.

هفت گناه کبیره:
هفت گناه کبیره گناهانی هستند که در زمان تاریخ بسیار قدیم رهبانیت مسیحی مشخص شده و در قرن ششم میلادی توسط پاپ گرگوری اول یا گرگوری کبیر در یک دسته قرار گرفته اند. این گناهان عبارتند از: تکبر، طمعکاری، شهوت در معنای تمایل بیش از حد یا نامشروع جنسی، حسادت، شکم پرستی که معمولا مستی نیز در آن منظور میشود و تنبلی. همف گناه کبیره از موضوعات مورد علاقه در وعظ و خطابه ها، نمایشنامه های اخلاقی و هنر اروپای قرون وسطی بوده است.

هفت کلمه آخر:
هفت کلمه آخر، به آخرین جمله حضرت عیسی بر صلیب اشاره دارد. این کلمات از این قرارند:
خدای من، چرا مرا به خود واگذاشتی؟

هفت علم انسانی ( علوم سبعه ):
طبقه بندی آزاد موضوعاتی که از قرن پنجم میلادی به بعد، دربرگیرنده برنامه آموزشی غرب در قرون وسطا بود. به نظر میرسد که نام "علوم انسانی" برگرفته از رساله "سیاست" ارسطو باشد که در آن از "شاخه هایی از دانش که شایسته انسان آزاد است" ، یعنی دانش اولیه ای که برای یک شهروند با تحصیلات مناسب لازم است، سخن گفته است. این علوم عبارتند از علوم سه گانه: دستور زبان ( ادبیات ) ، علم بیان و دیالکتیک ( مباحثه و مکالمه ) و علوم چهارگانه که پیشرفته تر بوده و از این قرارند: حساب، هندسه، موسیقی و نجوم.

عجایب هفتگانه طبیعی:
کوه اورست در مرز نپال و چین، آبشار ویکتوریا در آفریقا، گرند کنیون
Grand Canyon
آمریکا، ساحل مرجان بزرگ استرالیا، سپیده دم شمالی قطب شمال، آتشفشان و پاریکوتین
Paricutin
در مکزیک و بندر ریو دوژانیرو برزیل.

هفت مرد فرزانه:
نامی که در سنت یونانی به هفت تن از سیاستمداران، قانونگذاران و فیلسوفان قرن 7 و 6 قبل از میلاد داده شد. این فرزانگان عبارتند از: "سولون" قانونگذار یونانی، "تالس" فیلسوف اهل میلتوس، "پیتاکوس" فرمانده نظامی اهل میتیلن، "کلئوبولوس" فیلسوف اهل رودس، "شیلون اسپارتی" از ناظران شاه، "بیاس" فرزانه ترین هفت فرزانه، اهل پری ین و"پریاندر" حاکم مستبد کورنتی.

هفت دریا:
شامل دریاهای قطب شمال و قطب جنوب، اقیانوس آرام شمالی و جنوبی، اقیانوس اطلس شمالی و جنوبی و اقیانوس هند.

هفت حس:
بر اساس تعلیمات باستانی، روح انسان یا "بدن مقدس درون" او مرکب از هفت خاصیت است که هر یک تحت تاثیر یکی از سیارات هفتگانه اند. "آتش" موجب زندگی، "خام" به وجود آورنده توانایی احساس کردن، "آب" موجب قدرت بیان، "هوا" حس چشایی، "مه" موجد حس بینایی، "گلها" به وجود آورنده حس شنوایی و " باد جنوب" به وجود آورنده حس بویایی.

هفتمین پسر از هفتمین پسر:
همانطور که گفتیم هفت جادویی ترین اعداد است و در معرفت قومی، هفتمین فرزند پسر از هفتمین پسر یک خانواده با نیروهای قدرتمند جادویی و شفادهندگی متولد میشود. او پیشگو است و از قدرت های عجیبی برخوردار است.

عجایب هفتگانه قرون وسطی:
آمفی تئاتر روم، کاتاکومبهای (سرداب) اسکندریه مصر، دیوار بزرگ چین، استون هنج در ویلتشایر انگلستان، برج کج پیزا، برج چینی (از جنس چینی) نانکینگ، مسجد ایاصوفیه در استانبول.

هفت و…
نزد بسیاری از اقوام عهد باستان «هفت» عدد ویژه ای بود. در فلسفه و نجوم مصریان و بابلی ها، عدد هفت به عنوان مجموع هر دو زندگی، سه و چهار، جایگاه ویژه ای داشت.(پدر و مادر و فرزند؛ یعنی سه انسان، پایه و اساس زندگی هستند و عدد چهار مجموع چهار جهت آسمان و باد است.)
ایرانیان قدیم در آیین زرتشت، اهورامزدا را مظهر پاکی میدانستند و برای او هفت صفت را بر می شمردند و در مقابل او اهریمن را پدید آورنده ی پلیدیها می دانستند و می گفتند در پیرامون اهورامزدا فرشتگانی هستند که مظاهر صفات حسنه هستند و برای احترام به آن ها که اول هرکدامشان سین بود هنگام سال تحویل سفره می گستراندند و هفت قسم خوراکی که نام هریک با سین شروع می شود: سیر، سرکه، سیب، سماق، سمنو، سنجد، سکه، و سبزی را سر سفره می گذاردند که به سفره ی هفت سین معروف بود.

برای فیلسوف و ریاضیدان یونانی«فیثاغورث» نیز عدد هفت، مفهموم ویژه ی خود را داشت که از مجموع دو عدد سه و چهار تشکیل می شود: مثلث و مربع نزد ریاضیدانان عهد باستان اشکال هندسی کامل محسوب می شدند، از این رو عدد هفت به عنوان مجموع سه و چهار برای آن ها عدد مقدسی بود. علاوه بر این در یونان هر هفت سیاره را خدایی میدانستند : سلن، هیلیوس،آرس،هرمس، زئوس، آفرودیت و کرونوس.
یهودیان قدیم نیز برای عدد هفت معنای ویژه ای قایل بودند. در کتاب اول عهد عتیق (تورات) آمده است که خداوند جهان را در شش روز خلق کرد، در روز هفتم خالق به استراحت پرداخت. موسی در ده فرمان خود از پیروانش می خواهد که این روز آرامش را مقدس بدارند(روز شنبه و روز تعطیل یهودیان). علاوه بر این در آن کتاب مقدس هفت با عنوان عدد تام و کامل نیز استعمال شده است. از آن زمان عدد هفت نزد یهودیان و بعد ها نیز نزد مسیحیان که عهد عتیق را قبول کردند، به عنوان عددی مقدس محسوب می شد.

به این ترتیب بود که از دوران باستان هفتگانه های بیشماری تشکیل شدند: یونانیان باستان همه ساله هفت تن از بهترین هنرپیشگان نقش های سنگین و غمناک و نقش های طنز و کمدی را انتخاب میکردند. آن ها مانند رومی های باستان به هفت هنر احترام میگذاشتند. روم بر روی هفت تپه بنا شده بود. در تعلیمات کلیسای کاتولیک هفت گناه کبیره(غرور، آزمندی، بی عفتی، حسد، افراط، خشم و کاهلی) و هفت پیمان مقدس(غسل تعمید، تسلیم و تصدیق، تقدیس و بلوغ، ازدواج، استغفار و توبه، غسل قبل از مرگ با روغن مقدس، در آمدن به لباس روحانیون مسیحی) وجود دارد.

برای پیروان محمد(ص) آخرین مکان عروج، آسمان هفتم محسوب می شود. در بیست و هفتم ژوئن هر سال، روز «هفت انسان خوابیده » مسیحیان یاد آن هفت برادری را که در سال ۲۵۱ بعد از میلاد، برای عقیده و ایمان خود، زنده زنده لای دیوار نهاده شده و شهید شدند، گرامی می دارند؛ مردم عامه می گویند که اگر در این روز باران ببارد، به مدت هفت هفته بعد از آن هوا بد خواهد بود، آن گاه انسان باید هفت وسیله ی مورد نیازش را بسته بندی کند و با چکمه های هفت فرسخی خود به آن دورها سفر کند.

صور فلکی خوشه ی پروین یا ثریا به عنوان «هفت ستاره» معروف است، در حالی که حتی با چشم های غیر مسلح میتوان در این صورت فلکی تا یازده ستاره را دید. عرفای بزرگ عشق و وصال را در هفت مرحله و هفت وادی نشان داده اند و فاصله ی بین هستی و تباهی را پنچ مرحله دانسته اند.

در افسانه ها نیز با هفت سحر آمیز برخورد می کنیم: هفت هری پاتر (قسمت هفتم)،سوار ریش آبی هفت همسر داشت، سفید برفی با هفت کوتوله پشت هفت کوه زندگی می گرد و افسانه ی اژدهای هفت سر…

علاوه بر این می توان به هفت پلکان مقبره کورش بزگ،هقت اقلیم، هفت اورنگ، هفت دفتر شاهنامه، هفت پیکر، هفت هیکل، هفت گناه کبیره، هفت خان رستم، هفت الوان، هفت گنج،هفت تحلیل و هفت طواف (در اعمال حج) و… اشاره کرد و به این ترتیب بود که تعداد بیشماری هفتگانه در دنیا بوجود آمد و به عدد هفت تقدس خاصی بخشید

تعین سن و تعداد سکه های درون جیب دوست شما

- از دوستتان بخواهید سنش را دو برابرکند (البته به شما نگوید)!

- سپس آن را با 5 جمع کرده و در 50 ضرب نماید.

- در آخر تعداد سکه‌های موجود در جیبش را به عدد به‌دست آمده اضافه کند

 و اگر سکه‌ای نداشت مقداری اضافه نکند.

- حال عدد نهایی به‌دست آمده را به شما بگوید.

 

کلید:اکنون کافی است مقدار 250 را از عددی که دوست‌تان گفته کم کنید.

دو رقم سمت چپ عدد حاصل، سن دوست‌تان و دو رقم سمت راست آن،

تعداد سکه‌های موجود در جیب اوست!

این روش در صورتی که تعداد سکه‌ها کم‌تر از 100 باشد درست است

چرا ریاضیات می خوانیم؟



چرا ریاضیات می خوانیم؟

مجموعه: آیا می دانید ؟

 

 

ریاضی چیست؟

آیا میتوان علم ریاضی را در چند جمله معرفی کرد ؟ بدون شک معرفی علوم پایه بخصوص علم ریاضی که مادر همه علوم است، کار بسیار دشواری است. زیرا علم ریاضی از یک سو ذهنی و تجریدی و از سوی دیگر عملی میباشد و در نتیجه یک تعریف باید کلی باشد تا بتواند تمام ابعاد دانش ریاضی را در بر بگیرد.برای مثال « آندروگلیسون» ریاضی دان آمریکایی در معرفی علم ریاضی می گوید:

«ریاضیات علم نظم است و موضوع آن یافتن ، توصیف و درک نظمی است که در وضعیتهای ظاهراََ پیچیده نهفته است و ابزارهای اصولی این علم ، مفاههیمی هستند که ما را قادر میسازند تا این نظم را توصیف کنیم.»

 

دکتر دیبایی استاد ریاضی دانشگاه تربیت معلم تهران نیز در معرفی علم ریاضی میگوید:

« علم ریاضی، قانونمند کردن تجربیات طبییعی است که در گیاهان و بقیه مخلوقات مشاهده میکنیم.علم ریاضیات این تجربیات را دسته بندی وقانونمند کرده وهمچنین توسعه میدهد.»

 

دکتر ریاضی استاد ریاضی نیز در معرفی علم ریاضی می‌گوید: «ریاضیات علم مدل‌دهی به سایر علوم است. یعنی زبان مشترک نظریات علمی سایر علوم ، علم ریاضی می‌باشد و امروزه اگر علمی را نتوان به زبان ریاضی بیان کرد، علم نمی‌باشد.»

 

ریاضیات بر خلاف تصور بعضی از افراد یکسری فرمول و قواعد نیست که همیشه و در همه‌جا بتوان از آن استفاده کرد بلکه ریاضیات درست فهمیدن صورت مساله و درست فکر کردن برای رسیدن به جواب است و برای به دست آوردن این توانایی ، دانشجو باید صبر و پشتکار لازم را داشته باشد تا بتواند حتی به مدت چندین ساعت در مورد یک مساله ریاضی فکر کرده و در نهایت با ابتکار و خلاقیت آن را حل کند.

 

معرفی گرایش های ریاضی:

ریاضیات هنری است باستانی واز همان آغاز از جمله ذهنی ترین و در عین حال علمی ترین تلاشهای آدمی بوده است. یعنی از همان 1800سال پیش از میلاد که بابلیها در زمینه خواص تجریدی اعداد به پژوهش پرداختند، ریاضیات در کنار جنبه های ادراکی نظری ،به صورت ابزار که هر روز برای مساحی زمین، دریانوردی وساختن بناهای بزرگ مورد نیاز بود،به کار میرفت.

 

امروزه نیز به همین منوال است وشاید به همین دلیل ما در رشته ریاضی با دو گرایش ریاضی محض وکاربردی روبهرو هستیم.اما آیا میتوان این دو گرایش ریاضی را به طور کامل از یکدیگر مجزا کرد؟آیا میتوان گفت که ریاضی محض تنها یک فعالیت ذهنی است وهیچ کاربردی ندارد و در کنار آن ریاضی کاربردی، کاربرد ریاضیات را در علوم وفنون مختلف بررسی میکند وآیا طبق نظر «هارولدهاردی» ریاضیدان بزرگ انگلیسی، تنها باید به خاطر زیبایی ریاضیات ( ریاضیات محض ) به آن پرداخت واین علم هیچ ارزش علمی ندارد ؟

 

باید گفت که امروزه چنین دیدگاهی قابل قبول نیست بلکه به اعتقاد ریاضیدانها حتی ذهنی ترین حوزه های ریاضیات مثل هندسه، نظریه اعداد ومنطق نیز اهمیت علمی بسیاری دارد وبه همین دلیل نباید ریاضیات را به دو گرایش ریاضی محض وریاضی کاربردی تقسیم کرد.

 

 

 

 

ویژگی ها و توانمندی های لازم برای موفقیت در رشته ریاضی:

ریاضیدان، کاشف متهور ناشناخته ها است. عاشقی است که با شوری فراوان پا در وادی ناشناخته ها میگذارد وبا تلاشی تحسین بر انگیز وبه کمک ابزارهایی که در اختیار دارد ، تاریکیهای راه را روشن کرده وراه را برای دیگران هموار میسازد.به همین دلیل یک ریاضیدان قبل از هر چیز باید جرات قدم گذاری در وادی ناشناخته ها را داشته باشد. همچنین باید با صبرو حوصله زیاد وابتکار وخلاقیت مسائل وقضایای دانش ریاضی راحل کند.

 

چرا ریاضیات می خوانیم؟

چرا باید ریاضیات بخوانیم؟راجر بیکن، فیلسوف انگلیسی در سال 1267 میلادی پاسخ این سوال را این چنین داده است: «کسی که این کار را نکند نمی تواند چیزی از بقیه علوم و هر آن چه در این جهان هست بفهمد . . . چیزی که بدتر است این است که کسانی که ریاضیات نمی دانند به جهالت خودشان پی نمی برند و در نتیجه در پی چاره جویی برنمی آیند.» می توانم همین جا سخن را پایان دهم اما ممکن است بعضی ها فکر کنند که شاید خیلی چیزها در هفت قرن گذشته تغییر کرده باشد.

 

شاهدی تازه می آورم، پال دیراک از خالقان مکانیک کوانتومی، معتقد است که وقتی تئوری فیزیکی ای را پایه ریزی می کنید نباید به هیچ شهود فیزیکی اعتماد کنید. پس به چه چیزی اعتماد کنید؟ به گفته این فیزیکدان مشهور، فقط به برنامه ای متکی بر ریاضیات ولو این که در نگاه اول ربطی به فیزیک نداشته باشد.

 

در حقیقت، در فیزیک تمامی ایده های صرفا فیزیکی رایج در ابتدای این قرن کنار گذاشته اند در حالی که الگوهای ریاضی ای که به زرادخانه های فیزیکدان ها راه یافته اند به تدریج معنای فیزیکی یافته اند. در این جاست که قابل اعتماد بودن ریاضیات به روشنی رخ می نمایاند. بنابراین الگو سازی ریاضی روشی پربار برای شناخت در علوم طبیعی است .

 

موریس کلاین می نویسد: یونانی های قدیم واقعیت های دنیای اطراف خود را با علم ریاضیات منطبق می دیدند و حقیقت نمایی طرح کیهان را در ریاضیات می یافتند. آن ها بین قانون های طبیعت و قانون های ریاضی شباهت هایی را احساس می کردند که اکنون یکی از پایه های اساسی علوم را تشکیل می دهد. بعدها یونانی ها در شناخت طبیعت پیشتر رفتند و اعتقاد استواری پیدا کردند که جهان بر اساس قانون های ریاضی طراحی شده و دستگاه کنترل شده ای است، از قانون هایی پیروی می کند و برای بشر قابل درک است.

دست آخر این که ریاضیات موسیقی ذهن است پس باید آن را نواخت.

آیا می دانید؟

آیا می دانید؟

حروف انگلیسيA,B,C,D، در املای انگلیسی هیچ یک از اعداد 1 تا 99 دیده نمی شود؟

حرف D برای اولین بار در عدد 100 بکار می رود(Hundred)

حروف A,B,C در املای انگلیسی هیچ یک از اعداد 1 تا 999 دیده نمی شود.

حرف A برای اولین بار در املای عدد 1000 دیده می شود (Thousand)

حروف B,C در املای انگلیسی هیچ یک از اعداد 1 تا 999999999 دیده نمی شود.

حرف B برای اولین بار در املای عدد بیلیون بکار می رود . (billion)و حرف C هیچ وقت در املای اعداد انگلیسی بکار نمی رود.

انیمیشن بدست آوردن مساحت دایره

طنز ریاضی

طنز ریاضی

سؤال:ثابت کنید مجموعه اعداد طبیعی جالبه.(اثبات بروش استقراء)

جواب:یک-اولین عدد طبیعی است پس جالبه.دوتنهاعدداول زوج طبیعی است پس جالبه.

فرض استقرا: ا گر  nعدد جالبی باشد

حکم استقرا: ثابت میکنیم  n+1 عددجالبی است.

اثبات: فرض کنیدn+1  جالب نباشد . درآن صورت اولین عدد طبیعی خواهد بودکه جالب نیست درنتیجه

       n+1 به عنوان اولین عدد طبیعی ناجالب ،جالب خواهدبود. پس مجموعه اعداد طبیعی جالبه.

 

رقص مهندسی

رقص مهندسی