هدیه وب سایتهای اتحادیه انجمنهای علمی وآموزشی معلمان ریاضی ایران
و شورای خانههای ریاضیات ایران
«4 وجهی منتظم»
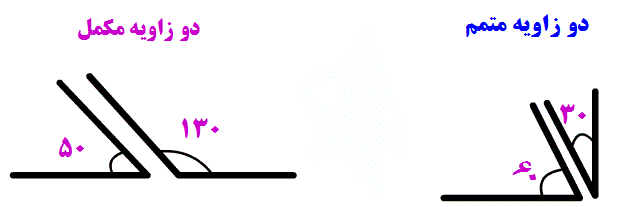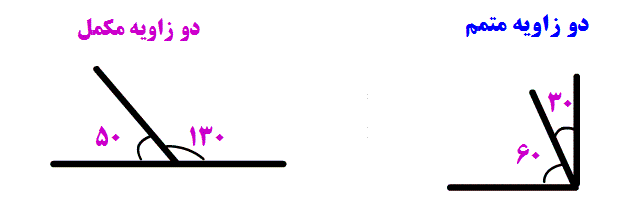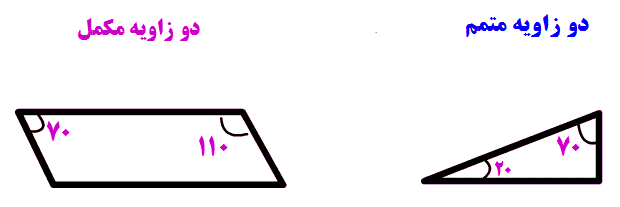
-نمایش زاویه های مکمل و متتم
انيميشن هاي رياضي
كارگاهي براي يادگيري اندازه گيري فاصله دو نقطه برروي مختصات
تمريني جالب براي يادگيري اعداد طبيعي
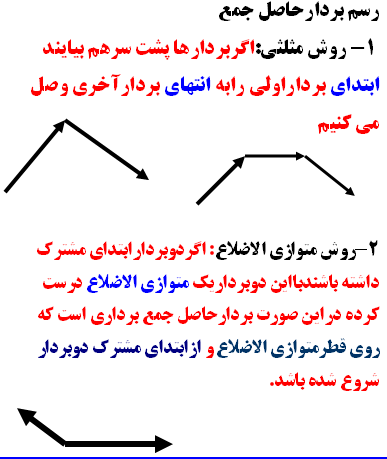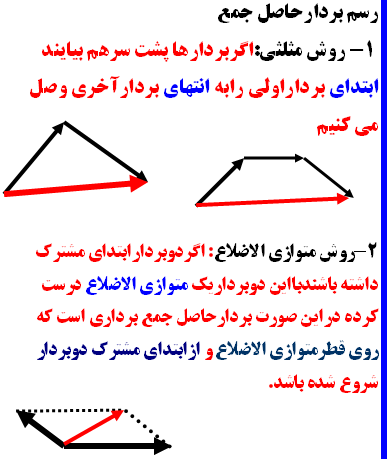
كارگاهي براي يادگيري جمع دو بردار
كارگاهي براي يادگيري جمع سه بردار
تمريني براي يادگيري عبارات جبري
كارگاهي براي يادگيري عبارات جبري
تمريني براي يادگيري عبارات جبري
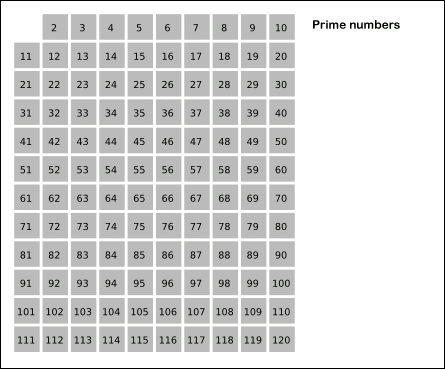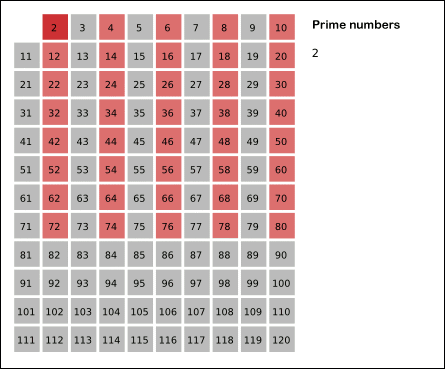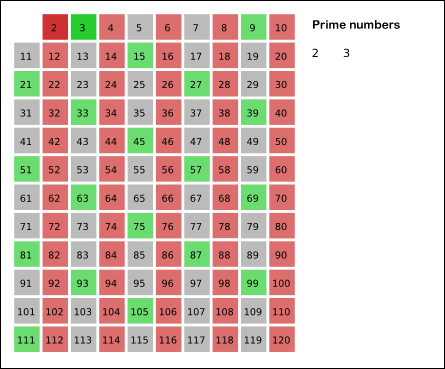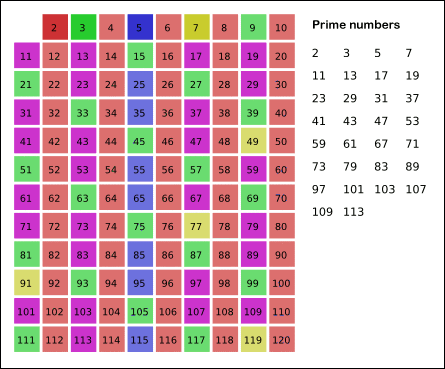
تمريني براي يادگيري اعداد اول ومركب
تمريني براي يادگيري تقارن برروي محور
تمريني براي يادگيري بردار واحد
كارگاهي براي يادگيري جمع دو بردار
این قضیه یکی از مهمترین قضایای کتابهای ریاضی دوره دبیرستان است که کاربرد زیادی در محاسبه حدود دارد.
قضیه ی فشردگی حدود:
اگر 
آن گاه : 
.(این قضیه برای حدهای یک طرفه و بی نهایت هم برقرار است.)
مثال: 
را بیابید.
با توجه به شکل زیر و استفاده از قضیه ی فشردگی ، نتیجه می شود که حد راست برابر ۰ است. برای بررسی حد چپ،کافی است نیمه ی دیگر نمودار تابع را در نظر بگیریم که مشابها” نتیجه می شود که حد چپ نیز برابر ۰ است و لذا حد مذکور برابر ۰ است .
راهنما استفاده :
۱-درگزينه بالا روی تست هوش آنلاین آبی رنگ كليك نمائيد .
۲- وارد سايت مي شويد .
۳- سمت چپ گزينه انگليسي را انتخاب نمائيد.
۴- مرحله بعد گزينه استارت (سمت راست ) انتخاب نمائيد.
۵- بعد از انجام تست براي مشخص شدن نمره سمت راست (پايين ) دکمه menu کلیک کرده و سپس سند
را بزنید .نمره هوش شما مشخص می شود .
حالا بگید در شکل زیر چند مثلث وجود دارد؟؟؟؟؟؟
علاوه بر مختصات دکارتی با همان محورهای مختصات که شما با آنها آشنا می شوید،مختصات هایی دیگر نیز وجود دارد از جمله مختصات قطبی که با چرخش یک محور در صفحه تصاویر زیبایی ایجاد می کند برای نمونه به تصویر زیر نگاه کنید:
تصاویری از پرندگان خشمگین در طبیعت
خطاي ديد به احساس ديدن تصاويري گفته ميشود که فريبنده يا گمراه کننده هستند. در اين حالت اطلاعاتي که بوسيله چشم جمع آوري شده و توسط مغز پردازش ميگردد منجر به درک تصويري ميشود که با واقعيت آن تصوير تطابق ندارد.
به اين تصوير نگاه کنيد. چه اتفاقي ميافتد؟ آيا اين حرکت دليل علمي دارد؟
خیلی جالبه پیشنهاد می کنم حتما امتحان کنید.
۳۰ ثانیه به نقطه ی قرمز (به صورت+) نگاه کنید سپس به جایی سفید مانند مانند دیوار نگاه کنید و زود پلک بزنید
بقیه ی تصاویر در ادامه مطلب
انیمیشن
آشنایی با مفهوم مكان هندسي و نمونه هايي از آن،درباره دایره،کره،کمان درخور،عمود منصف،..... در ادامه مطلب ببینید:
پاییز یعنی باران وباران یعنی شعر قشنگ گلچین گیلانی وخاطرات خوش کودکی
نفروئيد(Nephroid): اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع2 واحد، حول آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را نفروئيد گويند
ج)دلتاگون(Deltoid): اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع3 واحد، درون آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را دلتاگون گويند
د)ستاره گون(Astroid): اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع4 واحد، درون آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را ستاره گون گويند .
در ادامه مي توانيد روش
هاي ديگر رهيافت به اشكال فوق را ملاحظه نماييد :
توضیح:
۱) رنگ قرمز مضرب های مرکب ۲ را نشان می دهد.
۲) رنگ سبز مضربهای مرکب عدد۳ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)
۳) رنگ آبی مضربهای مرکب عدد۵ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)
۴) رنگ زرد مضربهای مرکب عدد۷ را نشان میدهد.(البته اونایی رو که قبلا خط نخورده اند)
۵) رنگ بنفش اعداد اول را نشان می دهد.
تقريب هندسي عدد پي
انيميشني كه روشي براي تقريب عدد پي ، ارائه مي كند ...
دايره اي به شعاع 1 واحد در نظر بگيريد . همان طور كه در شكل زير مي بينيم مساحت چند ضلعي هاي منتظم محاط در اين دايره با افزايش تعداد ضلع ها به سمت مساحت دايره كه همانا عدد پي مي باشد ، نزديك و نزديك تر مي شوند .یک انیمیشن بسیار جالب دیگر برای بدست آوردن مقدار تقریبی عدد پی:
تست هوش تصویری(درخت)
اگر بین ۰ تا ۵ تصویر صورت پیدا کردید – سبک مغز
اگر ۶ یا ۷ تصویر صورت پیدا کردید – کند ذهن
اگر ۸ یا ۹ تصویر صورت پیدا کردید – معمولی
اگر ۱۰ یا ۱۱ تصویر صورت پیدا کردید – خیلی خوب
اگر ۱۲ یا ۱۳ تصویر صورت پیدا کردید – نابغه
جالب بود!!! مگه نه؟
ترفندهای ضرب و تقسیم ریاضی (اعداد چند رقمی)
1 – عددهایی که به 5 ختم میشوند وضرب در مجذورشان می شوند؛ مثال: ؟ = 85×85
قدم اول: قسمت اول عدد را در بعلاوه یک همان عدد ضرب کنید ؛ 72 = (1+8)×8
قدم دوم: عدد 25 را جلو عدد بدست آمده تان بنویسید؛ 7225
تمرین: ؟ = 15×15 ---- ؟ = 65×65
1 - Square numbers ending in 5
85 x 85 = 7225
Step 1 - Multiply the first digit by the first digit plus one: 8 x (8 + 1) = 72
Step 2 - Write the number 25 next to the number from the first step: 7225
45 x 45 = 2025
Step 1 - 4 x (4 + 1) = 20
Step 2 – 2025
2 _ ضرب عددهای دورقمی در 11 ؛ مثال: ؟ = 11×53
قدم اول: دو رقم یکان و دهگان عددی که قرار است ضرب در 11 شود را با هم جمع کنید؛ 8 = 3+5
قدم دوم: عدد بدست آمده را بین دو رقمی که با هم جمع زدید قرار دهید؛ 583
تمرین: ؟= 11×78 ---- ؟= 39×11
2 - Multiply two digit number by 11
53 X 11 = 583
Step 1 - Add both digits of the two digit number: 5 + 3 = 8
Step 2 - Place the result in between both digits: 583
59 X 11 = 649
Step 1 - 5 + 9 = 14
Step 2 - Carry the 1 when the result is greater than 9: 5 + 1 = 6
Step 2 – 649
3 _ ضرب عددهای زوج در پنج؛ مثال: ؟ = 5×242
قدم اول: عدد ضرب شده در 5 را تقسیم بر 2نمایید؛ 121 =2÷242
قدم دوم: یک صفر آخر عدد بدست آمده در گام قبل قرار دهید؛ 1210
تمرین: ؟= 748×5 ---- ؟= 5×452
3 - Multiply even number by 5
242 x 5 = 1210
Step 1 - Divide the even number by two: 242 / 2 = 121
Step 2 - Put a 0 at the end of the result: 1210
4 _ ضرب اعداد بین 10 تا 19؛ مثال: ؟= 18×17
قدم اول: عدد بزرگتر را با یکان عدد کوچکترجمع کنید؛ 25 = 7+18
قدم دوم: یک صفر جلو نتیجه بدست آمده در مرحله قبل قرار دهید؛ 250
قدم سوم: یکان دو عددی که در هم ضرب شده اند را در هم ضرب نمایید؛ 56 = 8×7
قدم چهارم: جواب بدست آمده از مرحله دوم و سوم را با هم جمع نمایید؛ 306 = 250+56
تمرین: ؟ = 12×15 ---- ؟ = 19×16
4 - Multiply between 10 and 19
18 x 17 = 306
Step 1 - Add the larger number to the rightmost digit of the other number: 18+ 7 = 25
Step 2 - Put a 0 at the end of the result from step 1: 250
Step 3 - Multiply the rightmost digits of both original numbers: 8 x 7 = 56
Step 4 - Add steps 2 and 3: 250 + 56 = 306
5 _ تقسیم اعداد چند رقمی بر 5 ، 50 ، 500 و ... ؛مثال: ؟=5÷52
قدم اول: عددهایی را که تقسیم بر 5 ، 50 یا ... می شوند را ضرب در 2 کنید؛ 104 = 2×52
قدم دوم : جدا کنید عدد مرحله اول را با یک ممیز و به ازای هر صفر جلو 5 یک ممیز به عقب بروید؛ 10.4
تمرین: ؟=50÷482 ---- ؟= 5 ÷1150
5 - Divide by 5, 50, 500, etc..
52 / 5 = 10.4
Step 1 - Multiply the number being divided by two: 52 x 2 = 104
Step 2 - Shift the number from step 1 by one decimal point: 10.4
482 / 50 = 9.64
Step 1 - 482 x 2 = 964
Step 2 - Shift the number from step 1 by two decimal points (for dividing by 500 shift by three decimal points): 9.64
6 _ مجذور اعداد از ریشه 50؛مثال: ؟= 58×58
قدم اول:عدد یکان ضرب را با 25 جمع کنید؛ 33= 8+25
قدم دوم: عدد یکان را به توان 2 برسانید؛ 64= 8 ×8
قدم سوم: عدد بدست آمده در قدم دوم را جلو گام اول قرار دهید؛ 3364
تمرین: ؟= 51 ×51 ---- ؟= 59 ×59
6 - Square numbers in the 50's
58 x 58 = 3364
Step 1 - Add 25 to the ones digit: 25 + 8 = 33
Step 2 - Square the ones digit number: 8 x 8 = 64
Step 3 - Place the result from step 2 next to the result from step 1: 3364
7 _ ضرب اعداد دو رقمی که رقم دهگان شان شبیه به هم و عدد یکانشان بین 1 تا 9 متفاوت است؛مثال: ؟=38 ×32
قدم اول:عدد دهگان را ضرب در 1+ همان عدد نمایید؛ 12=(1+3)× 3
قدم دوم:یکان دو عدد را ضرب در هم نمایید؛ 16= 2 × 8
قدم سوم: نتیجه مرحله 2 را جلو مرحله یک قرار دهید؛ 1216
تمرین: ؟=75 ×79 ---- ؟= 43 ×44
7 - Multiply two digit numbers having same tens digit and ones digits add up to 10
38 x 32 = 1216
Step 1 - Multiply the first digit by the first digit plus one: 3 x (3 + 1) = 12
Step 2 - Multiply the rightmost digits (if the result is a single digit put a 0 in front of it): 8 x 2 = 16
Step 3 - Put the result from step 2 next to the result from step 1: 1216
8 _ ضرب در اعداد 9 ، 99 ، 999 و . . .؛ مثال: ؟=56 ×99
قدم اول: به ازای هر 9 انتهای عدد ضرب شده در 9 صفر قرار دهید؛ 5600
قدم دوم: عدد اولیه ی ضرب شده در 9 را ازعدد مرحله اول کم کنید؛ 5544=56-5600
تمرین: ؟= 48 ×99 ---- ؟=7 ×999
8 - Multiply by 9, 99, 999, etc..
56 x 99 = 5544
Step 1 - Place a zero at the end for each 9: 5600
Step 2 - Subtract the original number from step 1: 5600 - 56 = 5544
9 _ ضرب اعداد در 125 ؛ مثال: ؟=125 × 68
قدم اول: سه صفر آخر عدد ضرب شده در 125 قرار دهید؛ 68000
قدم دوم: عدد مرحله اول را تقسیم بر 2 نمایید؛ 3400= 2 ÷ 6800
قدم سوم:عدد مرحله دوم را تقسیم بر 2 نمایید؛ 1700= 2÷ 3400
قدم چهارم: عدد مرحله سوم را بر 2 تقسیم نمایید؛ 8500=2÷ 1700
یا داریم: (خلاصه مراحل)
قدم اول: سه صفر جلو عدد تک رقمی قرار داده؛
قدم دوم: عدد بدست آمده مرحله اول را تقسیم بر 8 نمایید؛
9 - Multiply by 125
68 x 125 = 8500
Step 1 - Place three zeros at the end of the number: 68000
Step 2 - Divide the number from step 1 by two: 68000 / 2 = 34000
Step 3 - Divide the number from step 2 by two: 34000 / 2 = 17000
Step 4 - Divide the number from step 3 by two: 17000 / 2 = 8500
10 _ مجذور اعداد در صورت دانستن مجذور عدد قبلی؛ مثال: ؟= 61 ×61
قدم اول: پیدا کنید مجذور عدد قبلی را ؛ 3600=60 ×60
قدم دوم: ضرب کنید عدد اولیه را در 2 سپس یک واحد از جواب بدست آمده کم نمایید؛ 121=1 - (61 ×2)
قدم سوم: مرحله 2 را با مرحله 1 جمع نمایید؛ 3721=3600+121
تمرین: ؟= 51 ×51 ---- ؟= 91 ×91
10 - Square numbers if you know the square of the previous number
61 x 61 = 3721
Step 1 - Find the square of the previous number: 60 x 60 = 3600
Step 2 - Multiply the number being squared by two and subtract one: (61 x 2) - 1 = 121
Step 3 - Add step 2 to step 1: 3600+ 121 = 3721
این مطلب ترجمه ای میباشد از نرم افزار شگفت انگیز Math Tricks Lite و شامل 10 ترفند اولیه این نرم افزار به همراه ترجمه میباشد ؛ تقدیم به تمام علم دوستان و دانشجویان و دانش آموزان؛
ثابتی که گاهی اوقات زیر آبی می رود!
در سال ۱۹۴۹ یک ریاضیدان هندی به نام «کاپرکار» ویژگی جالبی را در اعداد کشف و در مقالهای در همان سال منتشر کرد . او کشف خود را این طور توضیح دادهبود : یک عدد چند رقمی انتخاب کنید (مثلا ۸۹۵۲) ، ارقام آن را یک بار به صورت نزولی مرتب کنید (۹۸۵۲) و یک بار هم به صورت صعودی (۲۵۸۹) ، تا «بزرگترین» و «کوچکترین» عدد ، با همان ارقام حاصل آید.
با سلام و عرض ادب:
